EAS439 Lab Assignment Report: Numerical Analysis 2025
| University | Singapore University of Social Science (SUSS) |
| Subject | Numerical Analysis |
Lab Assignment Report
This assignment is worth 12% of the final mark for EAS439 – Numerical Analysis.
The cut-off date for this assignment is 30 March 2025, 2200 hr.
Note to Students:
1. Submit your report in the either in .doc or .pdf format before the submission cut-off date shown above in the CANVAS system.
2. You should prepare and submit this assignment as a formal report.
3. Accompanying excel file or Matlab file to show your calculation should also be submitted
4. Late submission will be subjected to the mark deduction scheme. Please refer to the Student Handbook for details.
5. Indicate your full name, student ID number and SUSS email address on the cover page of your report.
6. Name the MS Word file in the format:
“EAS439_LabR_YourFullName_YourStudentID.doc”.
Question 1
From the LU decomposition, one can derive the Jacobi and Gauss-Seidel numerical methods to iteratively solve the matrix equation
AX = b.
These methods are important because engineering problems such as those modelled by finite difference or finite element approaches often result in this matrix equation. Typically, the matrix A is too big and sparse for the equation to be solved by analytical methods efficiently.
(a) Compose a function in MATLAB that employs the Gauss-Seidel method to solve the equation above. Your function should accept two arguments: 1) the square matrix A of any size and 2) the RHS vector b. Use a stopping criterion of εs = 0.0001% for the approximation error and a maximum iteration number of 200. (6 marks)
(b) Calculate the solutions to the equations below using your code in part (a). Explain any modifications to each equation, if any.

(c) If your function in part (a) is to employ the Jacobi method instead of Gauss-Seidel, appraise and explain the changes you have to make to the code. (4 marks)
(d) Compute the solutions to the equations in part (b) again, this time using the Jacobi method. Which of the two methods has faster convergence? Explain a reason for the faster convergence. (4 marks)
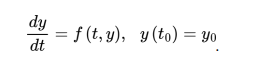
Hire a Professional Essay & Assignment Writer for completing your Academic Assessments
Question 2
The Runge-Kutta 4th-order (RK4) numerical method is a popular approach to solve ODEs of the form below due to its superior accuracy and stability over the Euler’s method.
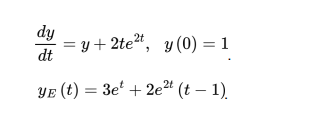
(c) If the Euler’s method is used instead to solve the ODE in part (b), appraise the relative true error of the numerical solution at tf. Which numerical method is more accurate? (4 marks)
(d) Compute the solution of the ODE below using your code in part (a) using a step size of h = 0.2 until tf = 6 and show the solution plot. Given that the exact solution is not known, explain how you would appraise the accuracy of the numerical solution at tf in this case.
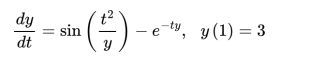
Question 3
The finite difference method is widely applied to solve PDEs numerically, such as the Poisson’s equation for steady-state 2D heat conduction
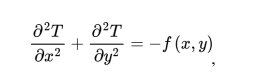
where f(x, y) represents a heat source.
(a) By discretizing the partial derivatives using central differences, formulate the GaussSeidel iterative formula to compute the temperature at node (i, j).
(6 marks)
b) Design and program a script in MATLAB that employs the formula in part (a) to compute the solution of the Poisson’s equation. The computational parameters and boundary conditions are given below. Terminate the computation when the largest temperature difference between successive iterations is less than 1xe-6 . Plot a 2D heatmap of the temperature field to show the results.
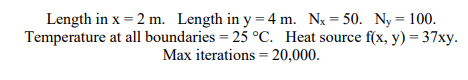
(8 marks)
(c) Analyze the temperature field in part (b) and explain if the solution is logical.
(6 marks)
(d) Appraise the accuracy of the solution in part (b) by performing a grid convergence analysis. That is, double the mesh and compute the solution again. Compare the temperature field and the highest temperature with those in part (b) and analyse. (4 marks)
(e) The boundary conditions are changed such that the right and top boundaries are thermally insulated. Show and explain the changes you have to make to the script in part (b). Compute the solution and show the temperature field. (6 marks)

(b) Formulate the finite-volume numerical scheme that is explicit in time to solve the convective equation in part (b). Define the fluxes at cell ij at time t illustrated below.
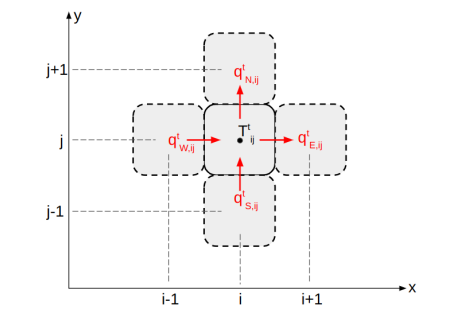
Buy Custom Answer of This Assessment & Raise Your Grades
- CH2123 Assignment: Fugacity, VLE Modeling & Applications of Henry’s Law
- BAFI1045 Assignment -Constructing and Evaluating Passive and Active Portfolios Based on the Straits Times Index (STI)
- FIN2210E/FIN2212E Group Assignment: Financial Risk Management Analysis of Bursa Malaysia Companies
- FLM101 Assignment: A Film Analysis: Stylistic Techniques and Their Thematic Importance
- HRM Assignment Answer: Talent Transformation in the Age of AI: Turning Challenges into Opportunities via Ecosystem Innovation
- COMP 1105 Assignment: Health-Focused E-Commerce Website: A Web Technologies Project Using HTML5, CSS, and JavaScript
- Assignment Anwser: Machine Learning in Robo-Advisory Services: Evolution, Applications, and Future Trends
- OMGT2229 Assignment: Quantitative EOQ Analysis, and Strategic Sourcing Decisions for JB Hi-Fi
- Assignment 2 Anwser: Corporate Finance and Planning: An In-Depth Financial Analysis of Company
- BUSM4551 Assignment: The Role of Innovation in Advancing the UN Sustainable Development Goals (SDGs)
UP TO 15 % DISCOUNT

