MTH316 TMA02: Multivariable Calculus Applications in Engineering
| University | Singapore University of Social Science (SUSS) |
| Subject | Multivariable Calculus |
TUTOR-MARKED ASSIGNMENT 02 (TMA02)
This assignment is worth 12% of the final mark for MTH316 Multivariable Calculus.
The cut-off date for this assignment is 20 March 2025, 2355hrs.
Note to Students:
You are to include the following particulars in your submission: Course Code, Title of the TMA, SUSS PI No., Your Name, and Submission Date.
For example, ABC123_TMA01_Sally001_TanMeiMeiSally (omit D/O, S/O). Use underscore and not space.
Question 1
The heat shield for the nose cone of a rocket is made from a composite material and has the solid region measured in meters defined by
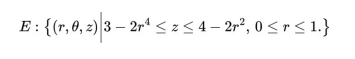
(a) Sketch the projections of the heat shield onto the Cartesian coordinate planes. Label all curves and intercepts clearly. (9 marks)
(b) Set up and calculate a triple integral in cylindrical coordinates that gives the volume of the heat shield. (10 marks)
(c) Without calculations, explain why the integral below does not give the volume of the heat shield. Using the same order of integration as the integral given below, evaluate an expression that gives the correct volume. You do not have to evaluate the integral/s. (10 marks)
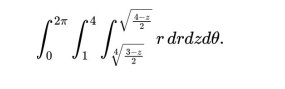
(d) The composite material used for the heat shield gives the density function in kg/m3 over region E as Set up and compute a triple integral that gives the total mass of the heat shield. (11 marks)
![]()
(e) The exterior parabolic surface of the heat shield is to be layered with a ceramic coating to lower its temperature during operation. Set up and calculate a double integral in cylindrical coordinates that gives the total surface area for the coating to be applied. (10 marks)
Hire a Professional Essay & Assignment Writer for completing your Academic Assessments
Question 2
During the manufacturing process of a semiconductor device, an inert gas is being used to protect the components from moisture and reactive oxygen. Jets of the inert gas impinges on the semiconductor surface and results in the pressure distribution in kPa below, where x and y are measured in cm.
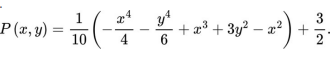
(a) Calculate the gradient of the function . Evaluate all critical points of the pressure distribution and calculate the pressures at all critical points. Apply derivative tests to classify all the critical points. (16 marks)
(b) Explain clearly if the pressure function has a global max and/or min if the domain is not restricted. State the global max and/or min pressure/s if any.
(6 marks)
(c) Over the region bounded by x and y axes and x + y = 1, the pressure has to be kept below 1.7 kPa due to some sensitive components. Find the highest pressure caused by the inert gas over the region and evaluate if the sensitive components are safe from potential damage during the manufacturing process. State any theorem used. (14 marks)
(d) A CPU chip is mounted flatly on the semiconductor device over the region – x y Calculate the force acting (downwards) on the CPU chip due to the inert gas. (8 marks)
(e) Without calculations, explain using a graph if the center of pressure of the force in partis at the center of the CPU chip. (6 marks)
Buy Custom Answer of This Assessment & Raise Your Grades
- Final Assignment: Migrating FashionOnline’s Infrastructure to AWS: A Strategy for Enhanced Availability and Data Protection
- HRM331: Talent Management – Strategic Shift from the War for Talent to the Wealth of Talent
- Marginalised Populations – The Structural and Cultural Exclusion of People Experiencing Homelessness in Singapore
- CVEN3501 Assignment 2: Groundwater Modelling of Drawdown from a Pumping Bore
- CSCI312 Assignment 2: Conceptual Modelling and Implementation of a Data Warehouse and Hive Queries
- CH2123 Assignment: Fugacity, VLE Modeling & Applications of Henry’s Law
- BAFI1045 Assignment -Constructing and Evaluating Passive and Active Portfolios Based on the Straits Times Index (STI)
- FIN2210E/FIN2212E Group Assignment: Financial Risk Management Analysis of Bursa Malaysia Companies
- FLM101 Assignment: A Film Analysis: Stylistic Techniques and Their Thematic Importance
- HRM Assignment Answer: Talent Transformation in the Age of AI: Turning Challenges into Opportunities via Ecosystem Innovation
UP TO 15 % DISCOUNT

